Yax2+bx+c
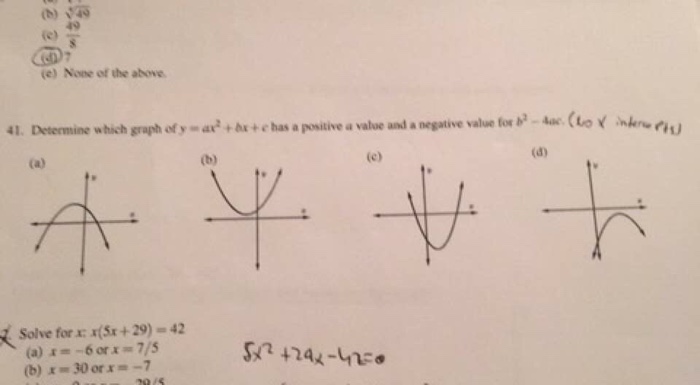
Solved Determine Which Graph Of Y Ax 2 Bx C Has A P Chegg Com

6 2 Solve Quadratic Equations By Graphing

Standard Form Y Ax2 Bx C Factored Form Y A X S X T

Solved A Quadratic Equation In The Form Y Ax 2 Bx C Chegg Com
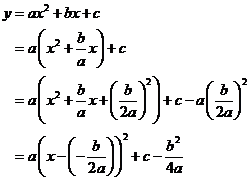
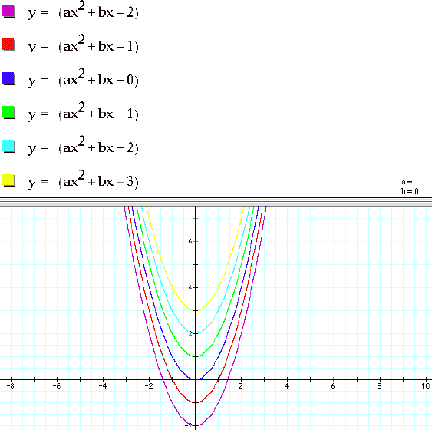
Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola

Graphing Y Ax 2 Bx C
Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
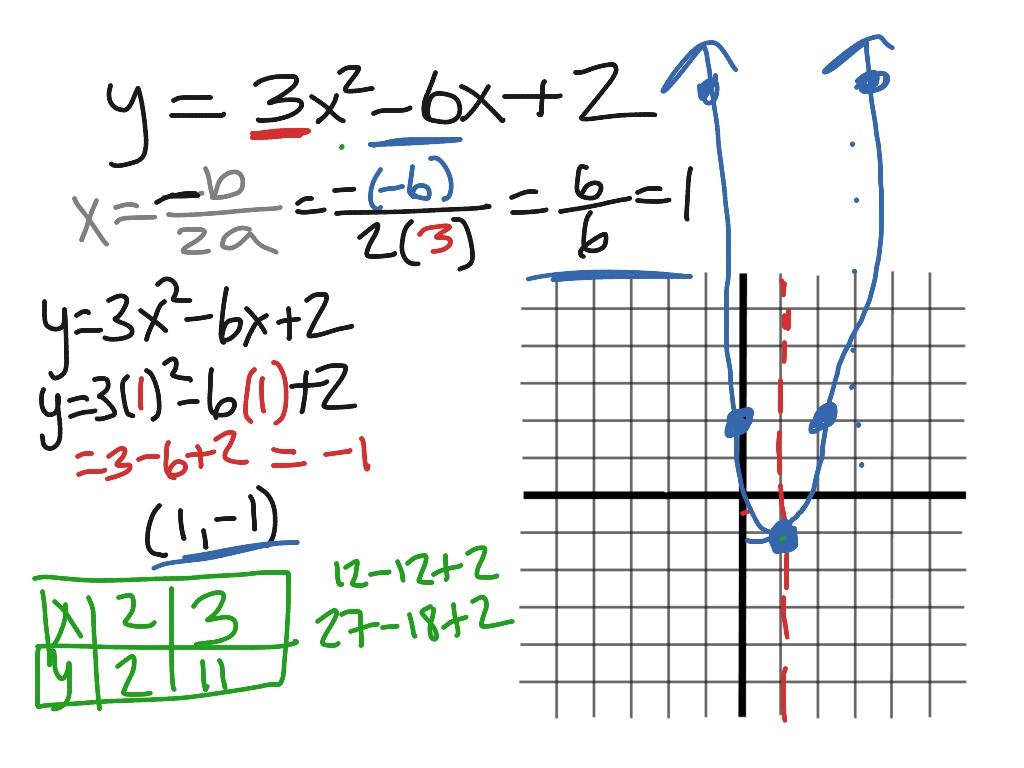
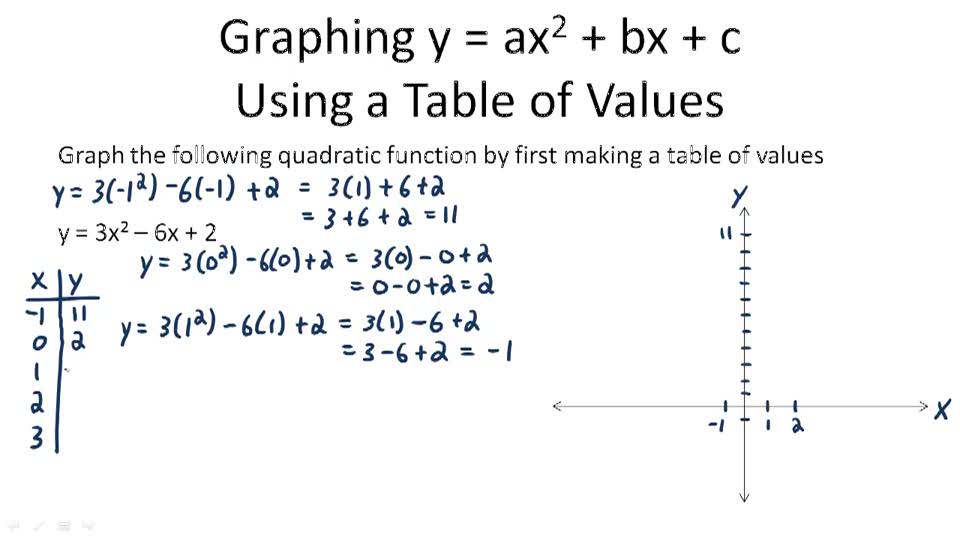
Yax2+bx+c. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with step-by-step explanations, just like a math tutor. Graph y = 2x2 - 4. How to Find the Vertex Slide 8:.
Free step-by-step solutions to Algebra 1:. Properties of Quadratic Functions in Standard Form Ax^2+Bx+C - Duration:. They are where the graph crosses the x-axis, or simply put, where y = 0.
Minimum Overview Determining if a Quadratic Function has a Maximum or Minimum. Complicated roots mean b² - 4ac < 0, i.e. The equation of the parabola y = ax2 + bx + c (1) The slope of the parabola are 6 at x = − 1 and −2 at x = 5.
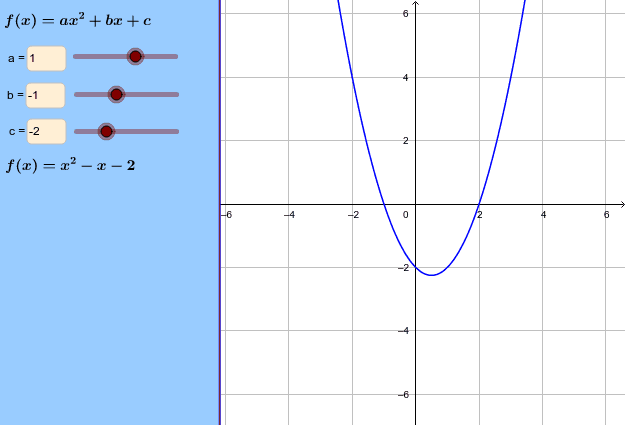
Y = ax 2 + bx + c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 + bx + c, where a, b, and c are rational numbers. Free quadratic equation calculator - Solve quadratic equations using factoring, complete the square and the quadratic formula step-by-step. Make room on the left-hand side, and put a copy of "a" in front of this space.
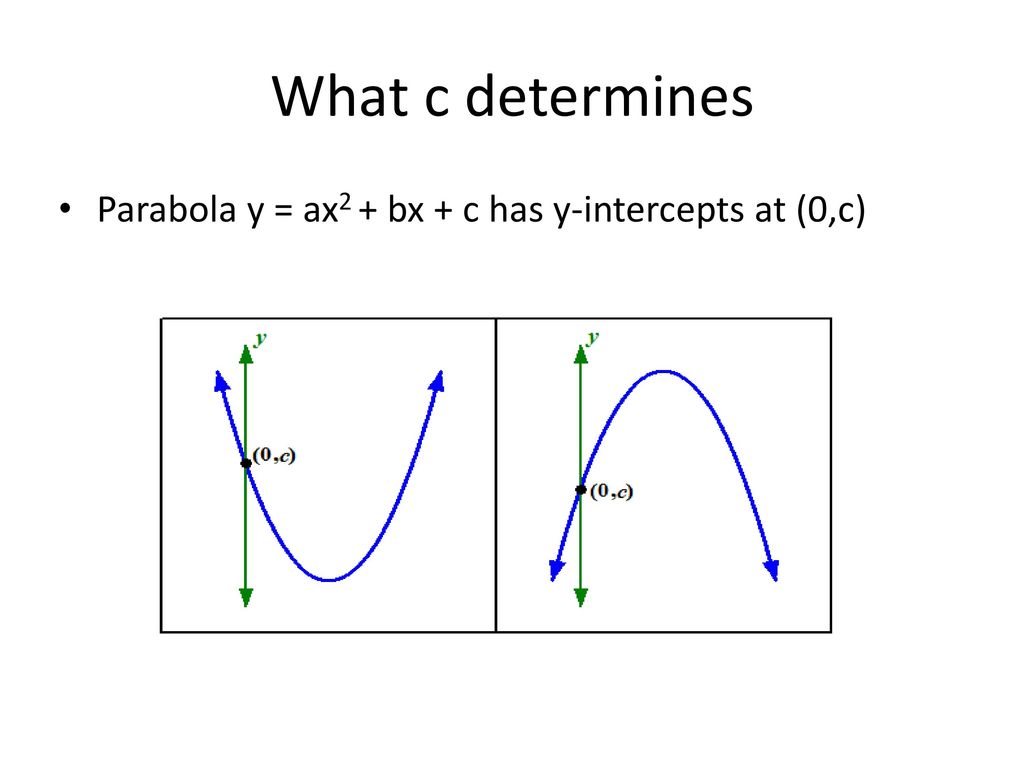
In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third. Complete the square of ax 2 + bx + c = 0 to arrive at the Quadratic Formula. If c is positive, there won't be any x-intercepts.
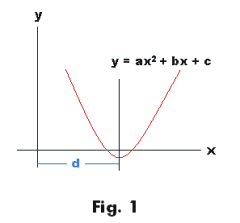
If c is negative, there won't be a y-intercept. The length of a tangent from the origin to the circle is :. Graphing y = ax2 + bx + cBy L.D.
Graph y = -x2 - Problem 7:. How to Find the the Direction the Graph Opens Towards Slide 6:. A parabola with equation \(y=ax^2+bx+c\) has a vertical line of symmetry at \(x=2\) and goes through the two points $(1,1)$ and $(4,-1)$.
Study this pattern for multiplying two binomials:. Y = x 2. Table of Contents Slide 3:.
If c is zero, the parabola will be centered around the y-axis. Ax 2 + bx + c = 0. So solving ax 2 + bx + c = 0 for x means, among other things, that you are trying to find x-intercepts.Since there were two solutions for x 2 + 3x – 4 = 0, there must then be two x-intercepts on the graph.Graphing, we get the curve below:.
Explorations of the graph. Yes, we can find it using infinitesimals. (f(x+epsilon) - f(x))/((x+epsilon) - x) = ((a(x+epsilon)^2+b(x+epsilon)+c)-(ax^2+bx+c))/epsilon = ((a(x^2+2epsilonx+epsilon^2)+b(x+epsilon)+c)-(ax^2+bx+c))/epsilon = ((ax^2+(b+2epsilona)x+(c+bepsilon.
A parabola y = ax 2 + bx + c crosses the x - axis at (α, 0) (β, 0) both to the right of the origin.A circle also passes through these two points. In a function of the form y= ax^2 +bx + c which of the following is always true?. Choose from 29 different sets of term:quadratic form = y = ax^2 bx+c flashcards on Quizlet.
But I'm not sure. For any quadratic equation of the form y = ax 2 + bx + c, the quadratic formula below. ALG 10.2 - Graph y=ax^2+bx+c - Duration:.
You can put this solution on YOUR website!. Rewrite so the left side is in form x 2 + bx (although in this case bx is actually ). Factor out whatever is multiplied on the squared term.
Y= ax^2 + bx +c. I'm dealing with quadratic equations (y=ax2+bx+c) and I need to know what the three variables, a, b and c stand for. It's a lot easier to look at it in the form.
X =-b ± b 2-4 a c 2 a. Suppose you have ax 2 + bx + c = y, and you are told to plug zero in for y.The corresponding x-values are the x-intercepts of the graph. The parabolic form of the equation which is y =a(x-h) 2 + k transforms into y = a(x-p) 2 + p because of the vertex being (h,k) = (p,p) To find a, we use the other condition the intercept is (0,-p).
Graph y = x Problem 2:. Its x-intercepts are rotated 90° around their mid-point, and the Cartesian plane is interpreted as the complex plane (green). A free graphing calculator - graph function, examine intersection points, find maximum and minimum and much more.
Y = ax^2 + bx + c is a parabola. A quadratic y = ax^2 + bx + c crosses the x-axis when the equation 0 = ax^2 + bx + c has at least one solution. Graph y = ½x Problem 4:.
Consequently a < 0 and c < 0 and now 4ac - 2bc + c² > b² - 2bc + c² = |b - c|² ?. Y – c = ax 2 + bx:. The formula h (t) = − 1 6 t 2 + 3 2 t + 8 0 gives the height h above ground, in feet, of an object thrown, at t = 0, straight upward from the top of an 8 0 feet building (a) What is the highest point reached by the object (b) How long does it take the object to reach its highest point?.
Y - k = a(x - h)^2 (note that the two a's aren't the same) in the second equation, the parabola has its vertex at (h,. Graph y = -x Problem 5:. (c) After how many seconds does the object hit the ground?.
The governing equation is y = -(2/p)x 2 + 4x -p so therefore, b = 4. Show that the tangent lines to the parabola y = ax 2 + bx + c at any two points with x-coordinates p and q must intersect at a point whose x-coordinate is halfway between p and q. Graph y = x2 - 40 Problem 6:.
We can find the slope using infinitesimals. Y=ax2+bx+cy=ax2+bx+c Rewrite the equationas ax2+bx+c=yax2+bx+c=y. Then, plug the X back.
To find the Y coordinate, plug it back in. • Find the vertex and x-intercepts of the graph. The greater root is \(\sqrt{n}+2\).
Y = ax 2 + bx + c:. Y=ax 2 +bx+c (-3,10) 10=a(-3) 2 +b(-3)+c 10=9a-3b+c (0,1) 1=a(0) 2 +b(0)+c 1=c (2,15) 15=a(2) 2 +b(2)+c 15=4a+2b+c. Recall that if there are solutions, they satisfy the quadratic formula.
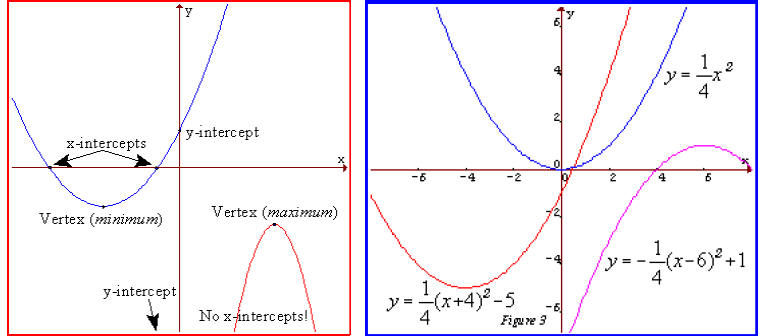
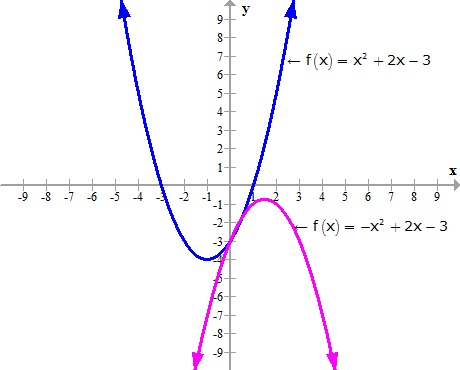
The following graphs are two typical parabolas their x-intercepts are marked by red dots, their y-intercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot:. By Kristina Dunbar, UGA. Graphing y = ax^2 + c 1.
$$3x^{2}-2x-8$$ We can see that c (-8) is negative which means that m and n does not have the same sign. I'm pretty sure c is the y-intercept, and I think b is used to partially calculate the turning point. The graph of y = ax^2 + bx + c A nonlinear function that can be written on the standard form a x 2 + b x + c, w h e r e a ≠ 0 is called a quadratic function.
B) Determine the following • Explain whether the graph has a maximum or minimum point. Graphing y = ax^2 + bx + c 1. Since the coefficient on x is , the value to add to both sides is.
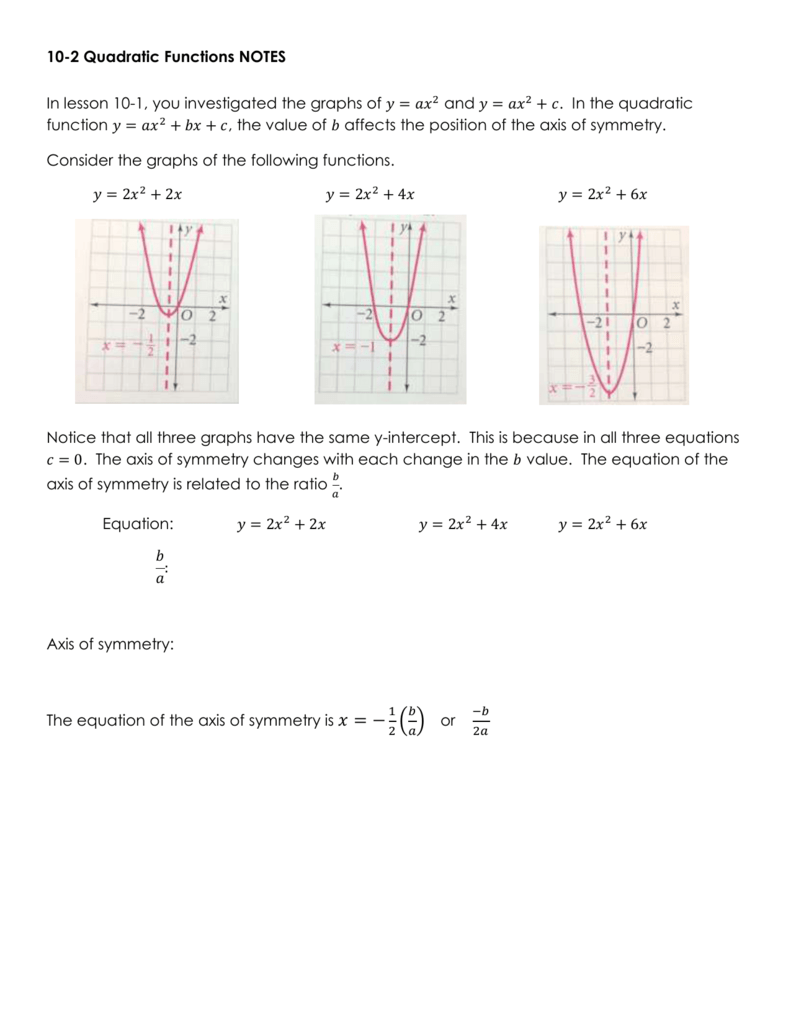
Enjoy the videos and music you love, upload original content, and share it all with friends, family, and the world on YouTube. If a > 0 and c > 0, then in accordance the nicely-conventional inequality we could have a + c ?. We learned from the video lesson that the b value in the quadratic equation y = ax 2 + bx + c affects the location of the parabola.
Improve your skills with free problems in 'Graphing y = ax 2 + bx + c Using the Vertex' and thousands of other practice lessons. Engaging math & science practice!. The graph of the function (fun.) y=ax^2+bx+c passes through the point (pt.) (3,1), so, the co-ordinates must satisfy the equation.
Let's use the information we learned in the lesson to find the. So substitute the value into the 1st and 3rd equations. {\displaystyle y=ax^ {2}+bx+c,} which is a parabola.
Visualisation of the complex roots of y = ax 2 + bx + c:. Graph y = ax^2 + bx + c. Graph y = 2x Problem 3:.
Problem 1 Slide 16:. The roots of a quadratic function are the same as its zeroes. The quadratic equation is given by:.
A) touches the x-axis at 4 and passes through (2,12) touches the x-axis at 4 means that passes trough (4,0) and b^2 - 4*a*c = 0 (the quadratic has 1 solution). We can change the quadratic equation to the form of:. If the parabola intersects the x -axis in two points, there are two real roots, which are the x -coordinates of these two points (also called x -intercept).
We now want to find m and n and we know that the product of m and n is -8 and the sum of m and n multiplied by a (3) is b (-2) which means that we're looking for two factors of -24 whose sum is -2 and we also know that one of them is positive and of them is negative. Let epsilon denote an infinitesimal. Tarver Academy 30,422 views.
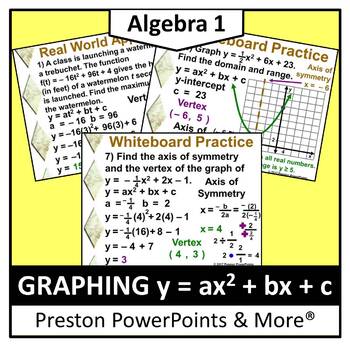
Graphing Quadratic Functions of the Form y = ax 2 + bx + c Overview Graphing y = ax 2 + bx + c Using a Table of Values Graphing y = ax 2 + bx + c Using the Vertex and Axis of Symmetry Analyzing Maximum v. A + c > b - contradiction. The parabola passing through the point (1, 4).
2?(ac) = ?(4ac) > ?(b²) = |b| ?. A is the coefficient of the x^2 term b is the coefficient of the x term c is the constant term they are used in equations to find the roots and in equations to find the minimum / maximum point of a quadratic equation and in equations to find the slope and y-intercept of a straight line, among other uses that I am probably not totally aware of. Y = ax 2 + bx + c.
For the first positions, find two factors whose product is 2 x 2.For the last positions, find two factors whose product is –12. Factor 2 x 2 – 5 x – 12. The quadratic \(ax^2 + bx +c\) has two real roots.
Ok, simple question, having trouble understanding this in school. Let f(x) = ax^2+bx+c Then the slope at x is the standard part of:. The graph of a quadratic equation in two variables (y = ax2 + bx + c) is called a parabola.
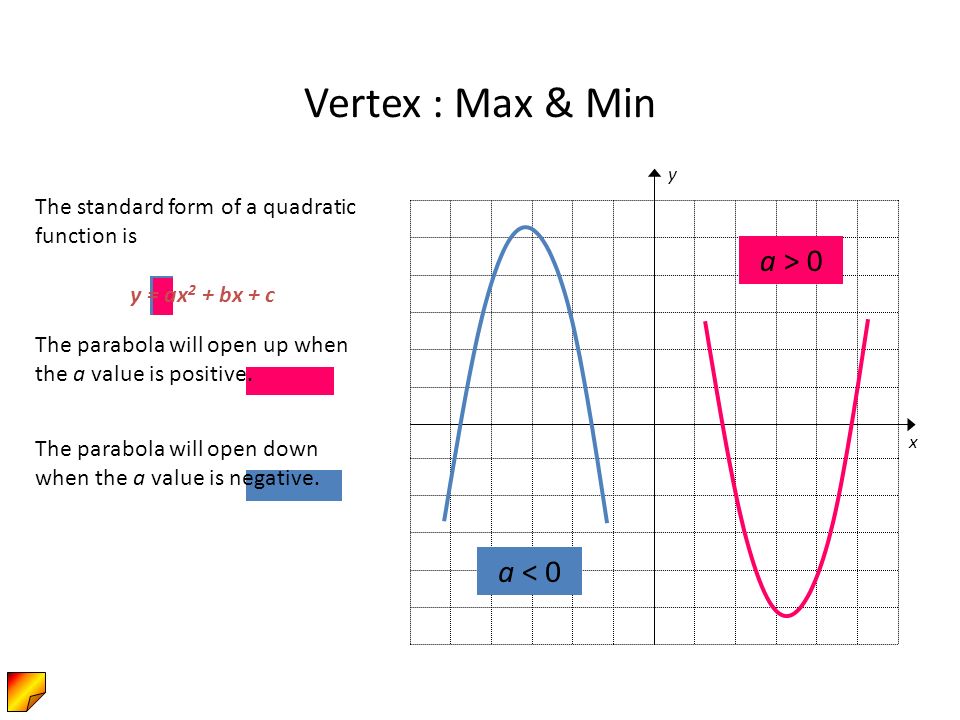
If a is positive, the parabola will have a minimum value. Divide both sides of the equation by a, so that the coefficient of x 2 is 1. A quadratic function can have 0, 1, or 2 roots.
B² < 4ac, consequently ac > 0 (a and c have comparable sign). So given a set of 3 points (xy-plane), such as (40,30) (60,28) (,25) i have to find the equation of the parabola. Learn term:quadratic form = y = ax^2 bx+c with free interactive flashcards.
We have split it up into three parts:. Begin by writing two pairs of parentheses. Now if you would like to do this the calculus way, differentiate the equation, and set the resulting 2ax = -b and solve for X.
How to Find the y Intercept Slide 7:. Move the loose number over to the other side. Problem 2 Slide 22:.
Powered by $$ x $$ y $$ a 2 $$ a b $$ 7 $$ 8. From the 2nd equation, we know that c=1. The x value halfway between the x-coordinate p and q.
When you substitute, you get a = -(2/p) So the parabolic equation is. Will find the roots, or zeroes, of the equation. (4a - 2b + c)c > 0, the.
The parabola is rotated 180° about its vertex (orange). 15=4a+2b+c 15=4a+2b+1 14=4a+2b. Of that vague equation, the X coordinate is at -b/2a.
Quadratic equation is a second order polynomial with 3 coefficients - a, b, c. A Common Core Curriculum () - Slader. The solution to the quadratic equation is given by 2 numbers x 1 and x 2.
Ax2+bx+c=yax2+bx+c=y Move yyto the left side of the equationby subtracting it from both sides. How to Find the Axis of Symmetry Slide 9:.

Let F X Ax2 Bx C Consider The Given Diagram Then
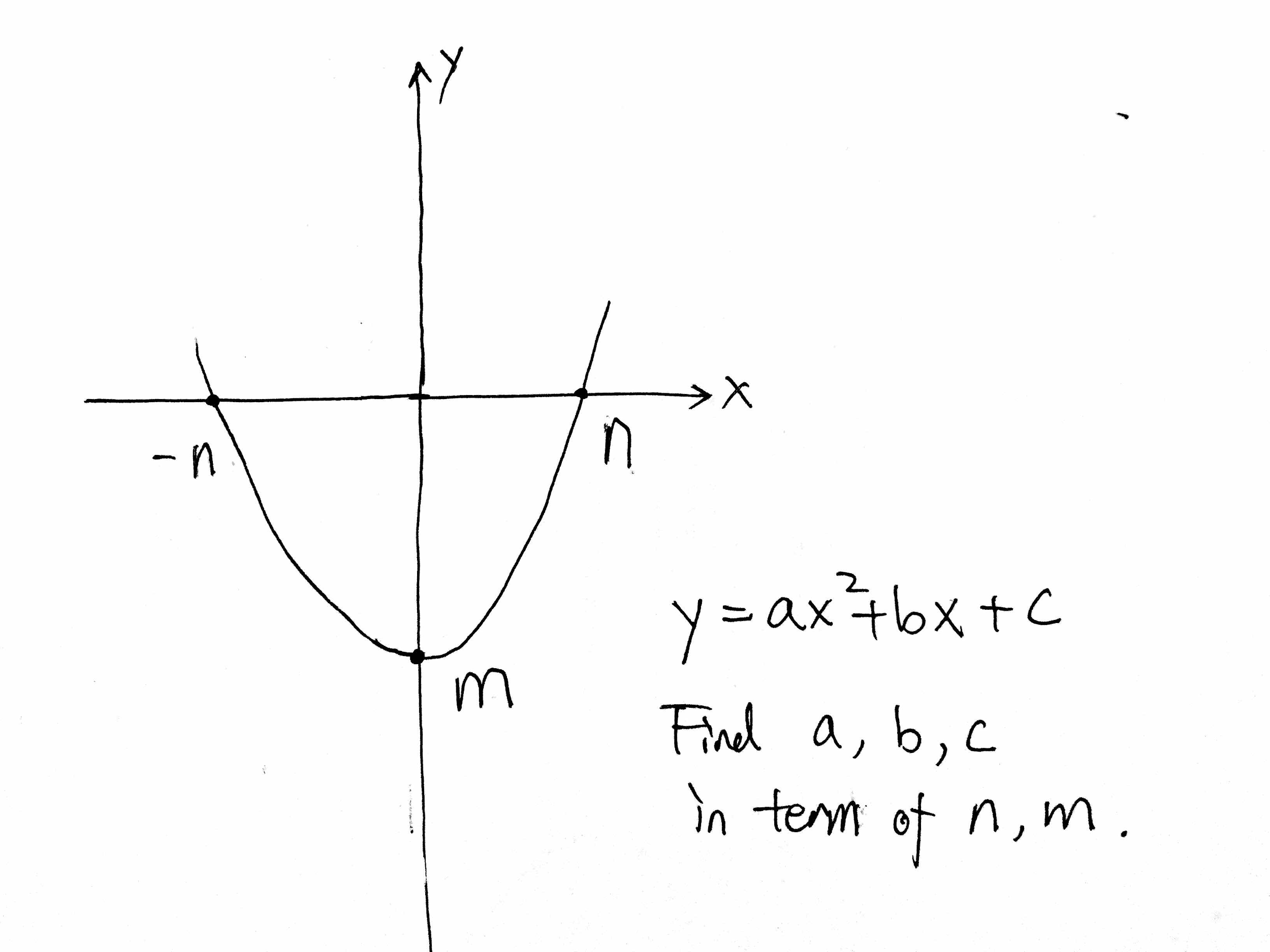
Solved Y Ax 2 Bx C Find A B C In Term Of N M Chegg Com

Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego
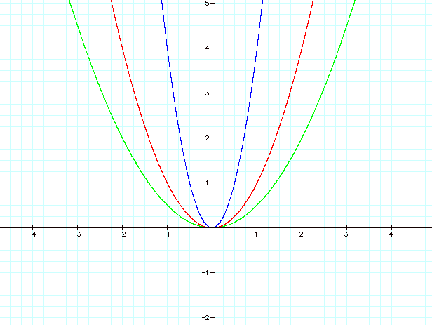
Examining The Parabola Assignment 2
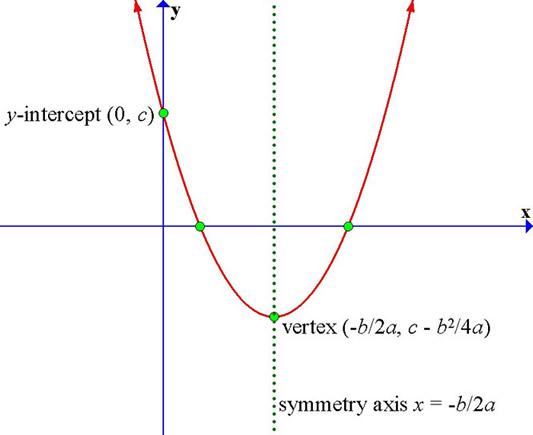
Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola
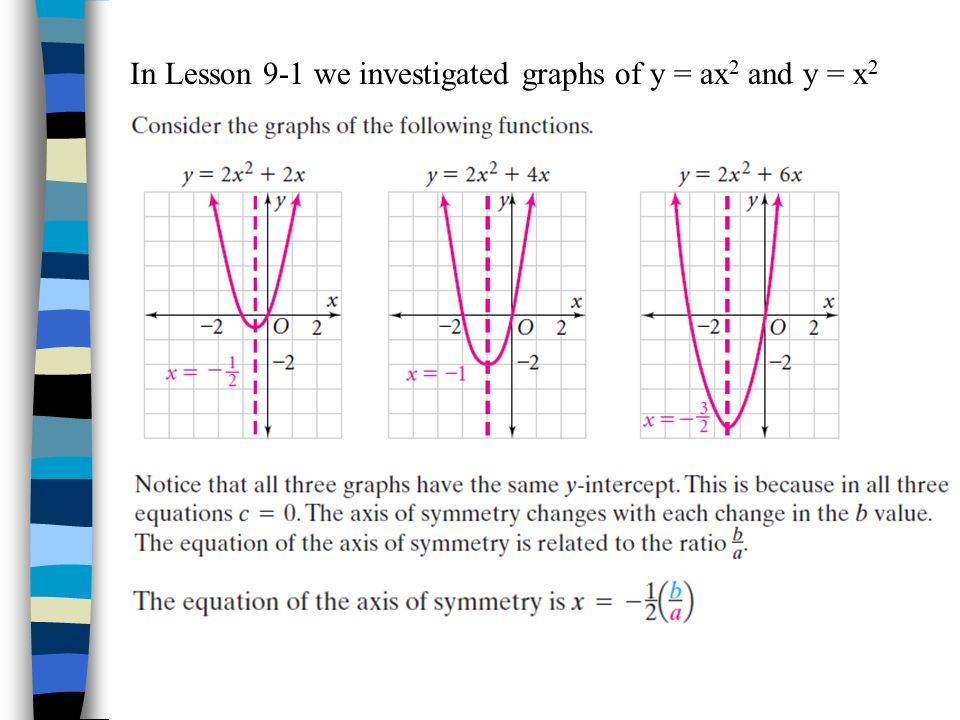
Lesson 9 2 Graphing Y Ax Bx C Objective To Graph Equations Of The Form F X Ax Bx C And Interpret These Graphs Ppt Download
Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id
The Function F X Y And Associated Matrices E And E

View Question A Parabola With Equation Y Ax 2 Bx C Has A Vertical Line Of Symmetry At X 1 And Goes Through The Two Points 1 3 And 2 2 The Quadratic
Linear Algebra Webnotes Class Assignments Chapter 1

Fillable Online Ms Algebra Ch 9 6 Factoring Ax2 Bx C Weebly Fax Email Print Pdffiller

Ppt Expanded Form Y Ax 2 Bx C Powerpoint Presentation Free Download Id 322

Graphing Y Ax2 Bx C Youtube
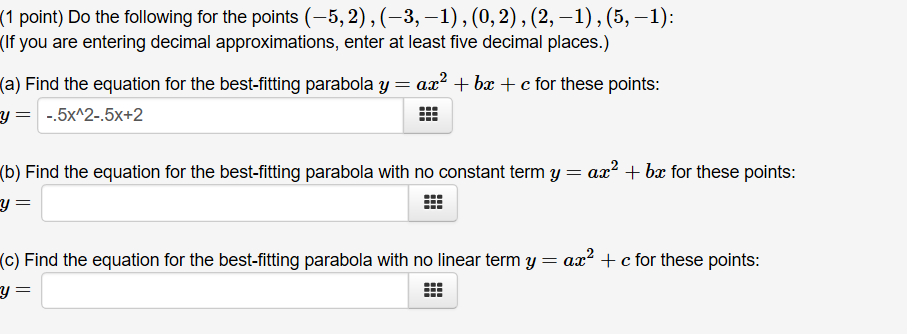
Solved Find The Equation For The Best Fitting Parabola Y Chegg Com
If Y 2 Ax 2 Bx C Then Y 3 D 2y Dx 2 Is A A Constant Sarthaks Econnect Largest Online Education Community
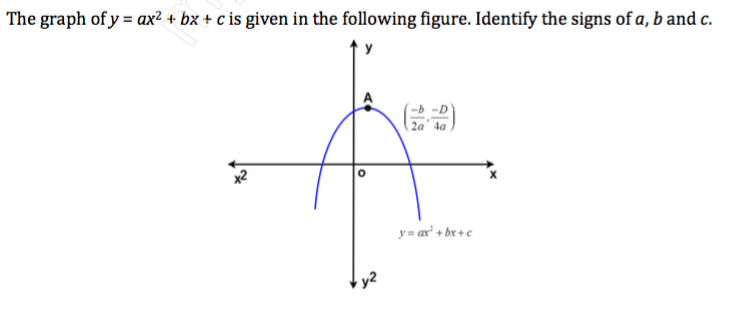
Solved The Graph Of Y Ax 2 Bx C Is Given In The Fol Chegg Com
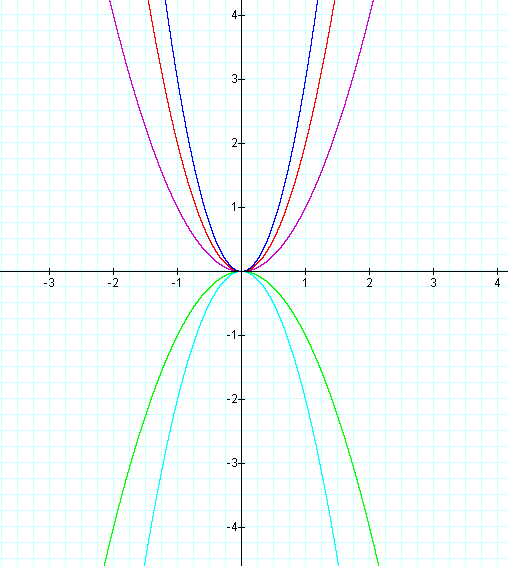
Exploring Parabolas Y Ax 2 Bx C

Prostate Gland Red And The Defined Pz Below Y Ax 2 Bx C Green Download Scientific Diagram
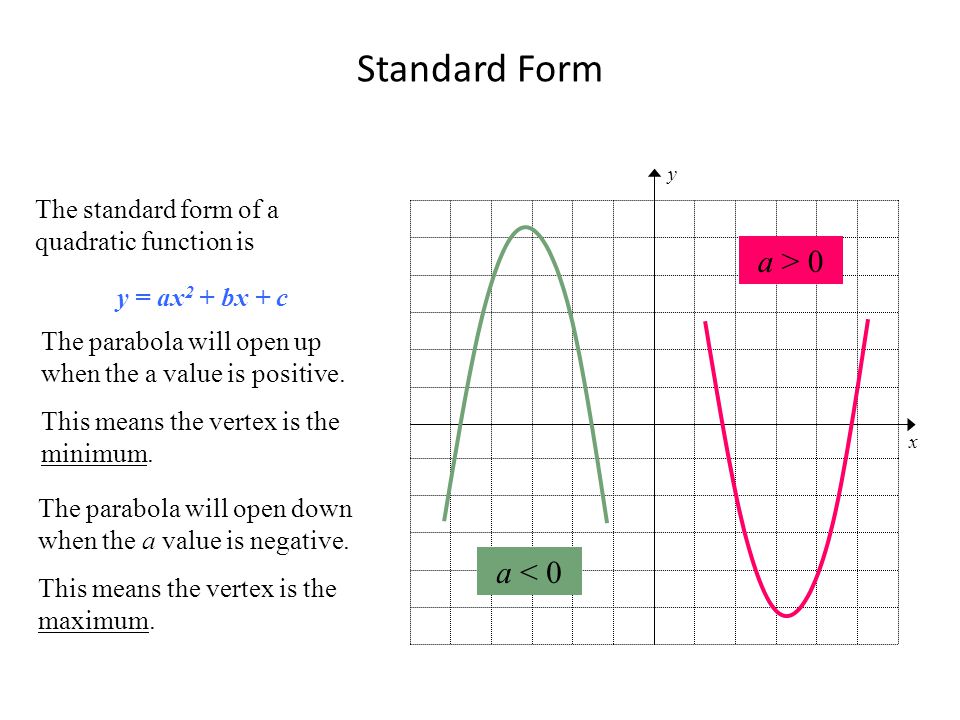
Topic U2 L1 Parts Of A Quadratic Function Graphing Quadratics Y Ax 2 Bx C Eq Can I Identify The Vertex Axis Of Symmetry X And Y Intercepts Ppt Download

Solved Find The Formula In Standard Formm Y Ax2 Bx Chegg Com
Equations And Graphs
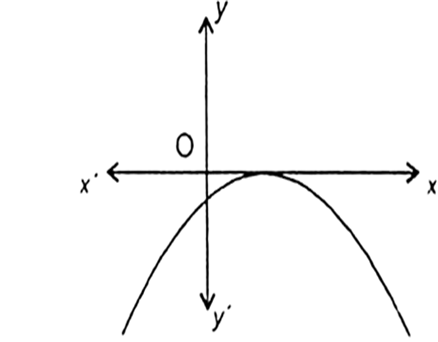
The Graph Of The Polynomial Y Ax2 Bx C Is Shown In Fig 2 2 Write The Value Of B2 4ac Y Ax2 Bx C From Mathematics Polynomials Class 10 Haryana Board English Medium

The Graph Of A Quadratic Function Y Ax 2 Bx C Is Shown Tell Whether The Discriminant Of Ax 2 Brainly Com
Q Tbn 3aand9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau
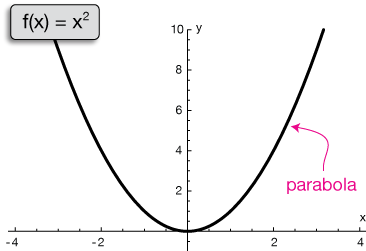
Quadratic Function Y Ax2 Bx C When A Is Sutori

The Graph Of Y Ax 2 Bx C Is Shown Below Determine The Solution Set Of 0 Ax 2 Bx C 1 Brainly Com

Y Ax2 Bx C Quadratic Function Quadratic Term Linear Term Ppt Download

Graphing Quadratic Functions Y Ax 2 Bx C Graphing Quadratic Functions Today We Will Understand How The Coefficients Of A Quadratic Function Influence Ppt Download
The Graph Of Y Ax 2 Bx C Geogebra

Graphing Quadratics
The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet
Differentiate The Function Y Ax 2 Bx C Youtube
Graph Of A Quadratic Function

How To Speak Y Ax 2 Bx C Englishteststore Facebook

Intro Intro We Already Know The Standard Form Of A Quadratic Equation Is Y Ax2 Ax2 Ax2 Ax2 Bx Bx C The The Constants Constants Are A B C
10 2 Graph Ax 2 Bx C Math Showme
Assignment 2

Unique Quadratic Equation In The Form Y Ax 2 Bx C

Graphing Y Ax 2 Bx C

0101 Graphing Quadratic Functions

Assignment 2
How To Draw A Parabola Ppt Download

Regression Analysis Of The Relationship Y Ax 2 Bx C Between Download Table
Q Tbn 3aand9gctktb4oj Ybnnap2fvmhphtzkozkn47g8uxfn2lg 8 Usqp Cau
Graph Quadratic Functions And Equations Video Algebra Ck 12 Foundation

Ppt Graphing General Quadratics Y Ax 2 Bx C Powerpoint Presentation Id
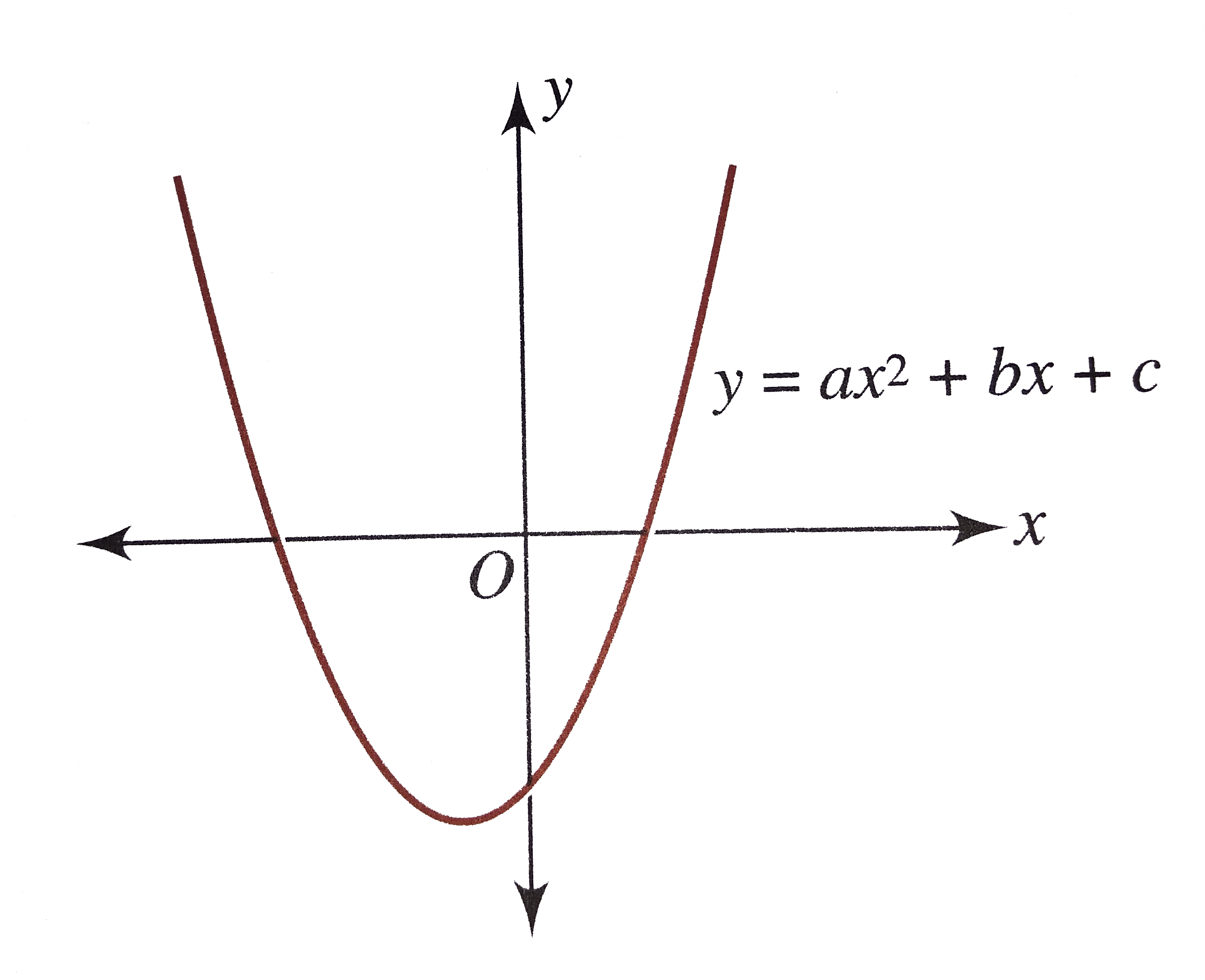
For Following Graphs Of Y Ax 2 Bx C With A B C C R Commen
The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora

The Graphs Of Y Ax2 Bx C Are Given In Figure Identify The Signs Of A B And C In Each Of The Following
Q Tbn 3aand9gcsjmhnpznkqqcgfrtj9zmgdmzwkdgrtso1ffgs6ifw2rrq3iitl Usqp Cau
If Y Ax 2 Bx C Represents A Parabola With Vertex A As Shown In The Figure And B 2 2 B 2ac Sarthaks Econnect Largest Online Education Community

Quadratic Formula Wikipedia
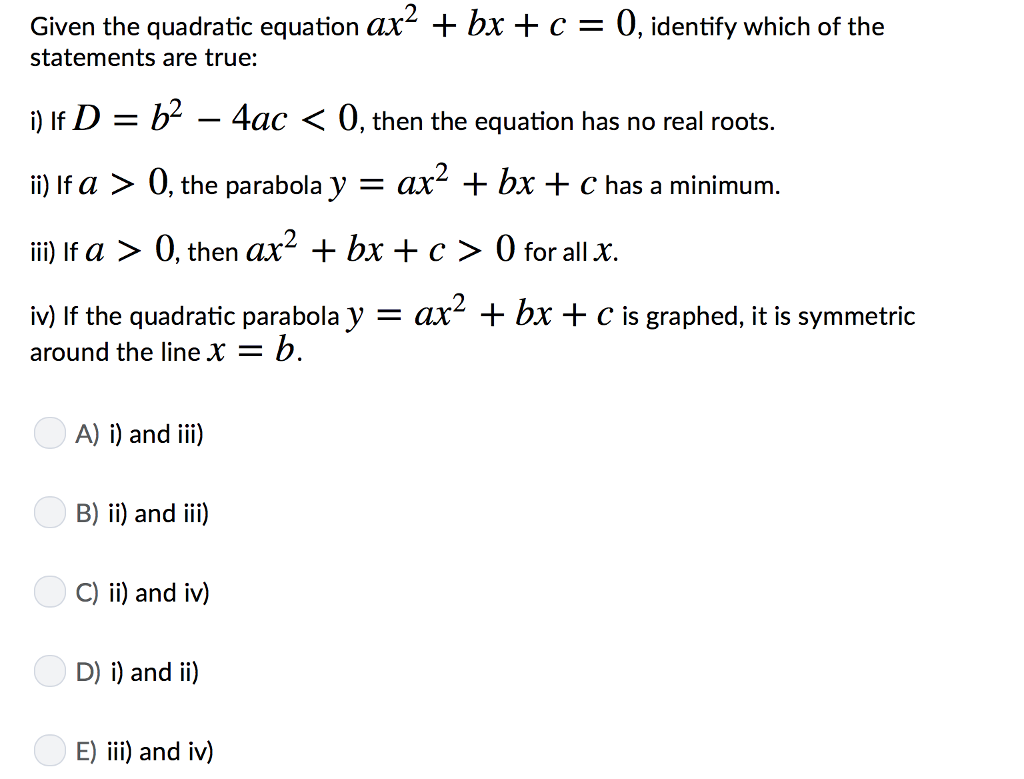
Solved Given The Quadratic Equation Ax2 Bx C 0 Ident Chegg Com

Consider The Graph Of Quadratic Polynomial Y Ax2 Bx C As Shown Below Which Of The Following Is Are Correct
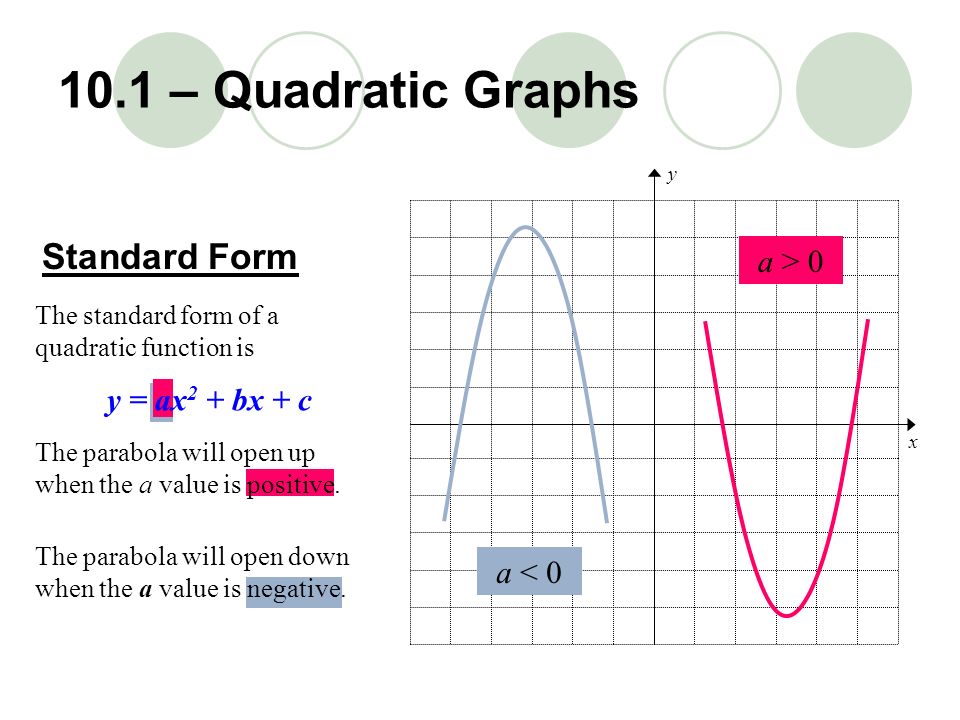
10 1 Quadratic Graphs Ppt Download
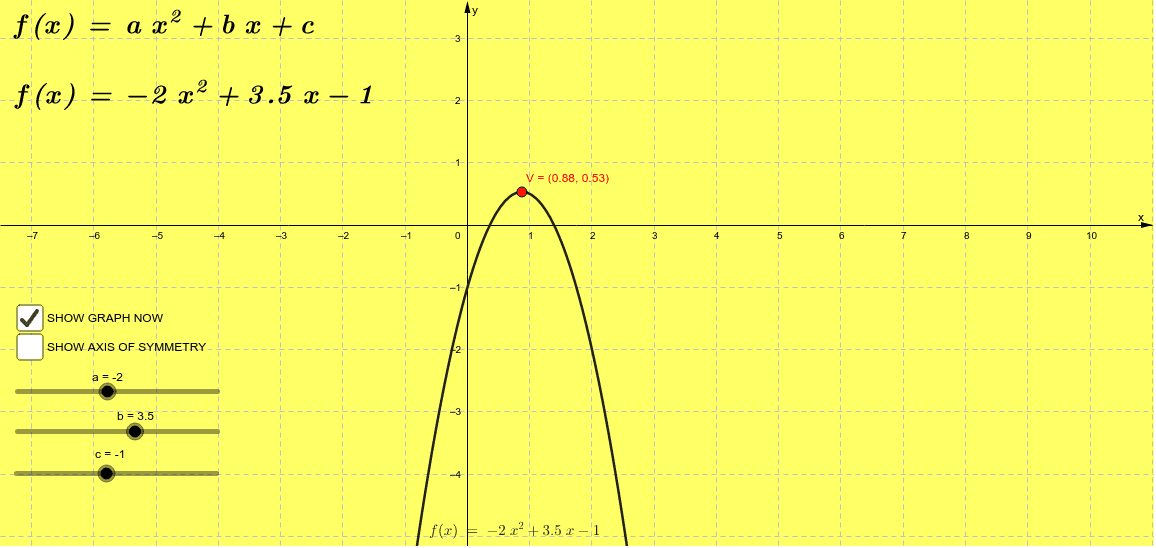
The Quadratic Function Y Ax2 Bx C Geogebra

Graphing Quadratic Functions Y Ax 2 Bx C Quadratic Functions The Graph Of A Quadratic Function Is A Parabola A Parabola Can Open Up Or Down If Ppt Download

Graphing Quadratics
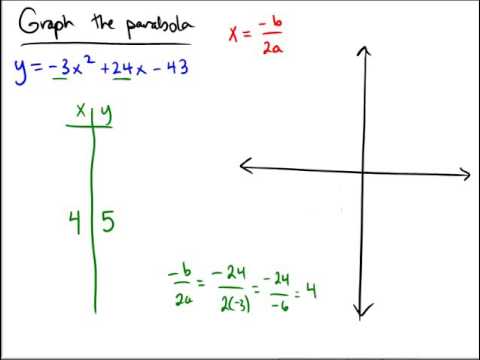
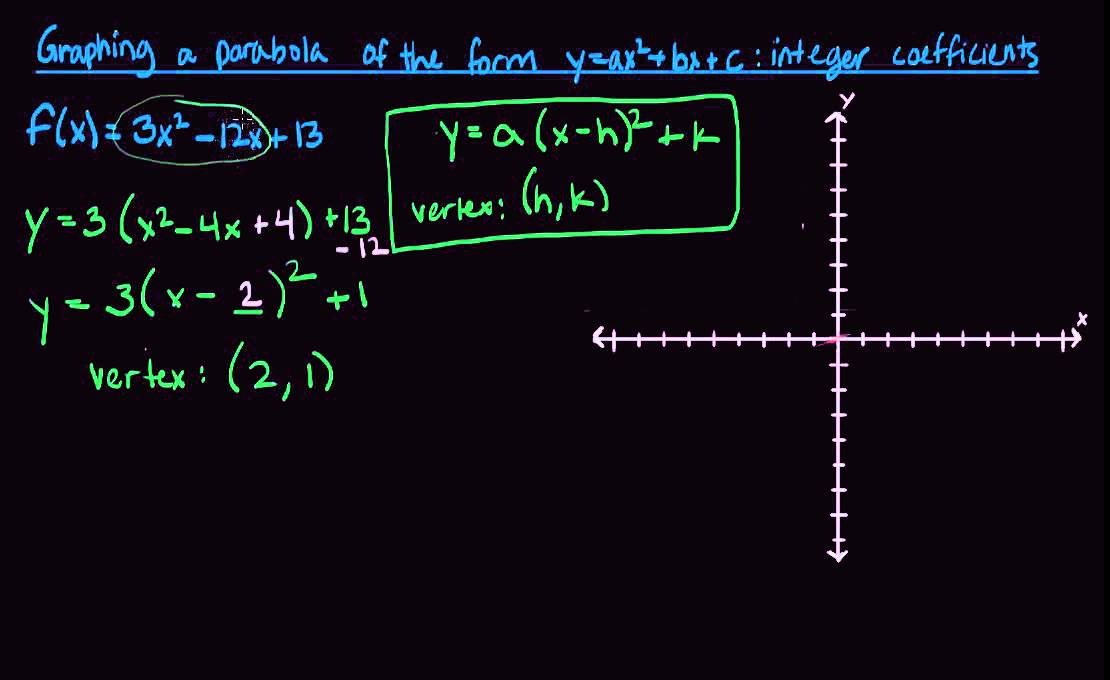
Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube

Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube
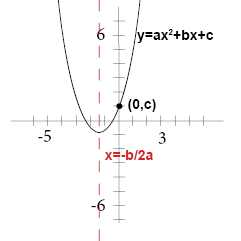
The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet

To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com

Solved Use The Graph Of Y Ax2 Bx C To Solve A Quadr Chegg Com

Parameter Values And Fit Goodness Of Polynomials Y Ax 2 Bx C Download Table
Q Tbn 3aand9gcr2d4gqdlharo4o5lj4yztsap5h9micavn2tzoyofc Usqp Cau
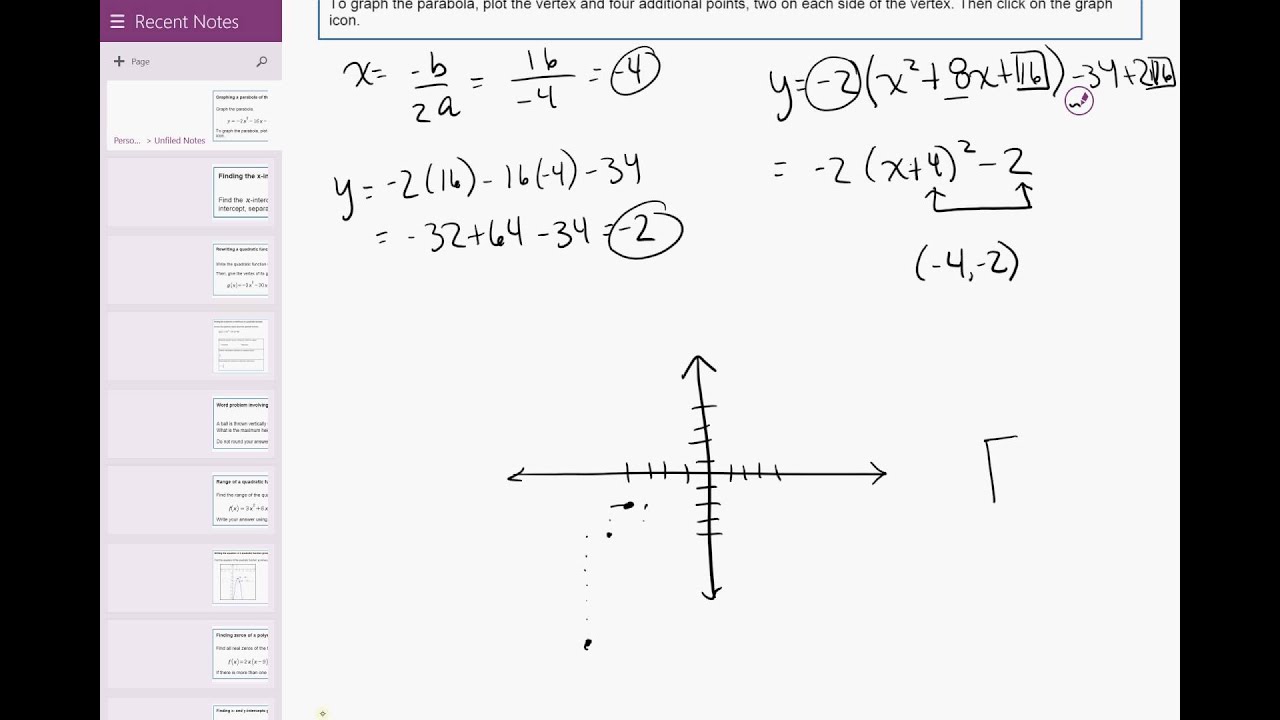
15 04 Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube
Solution Draw A Sketch Graph Of Y Ax 2 Bx C If A Lt 0 B Lt 0 C Lt 0 Discriminant 0

Solved Quadratic Equation Y Ax 2 Bx C Passes Throug Chegg Com
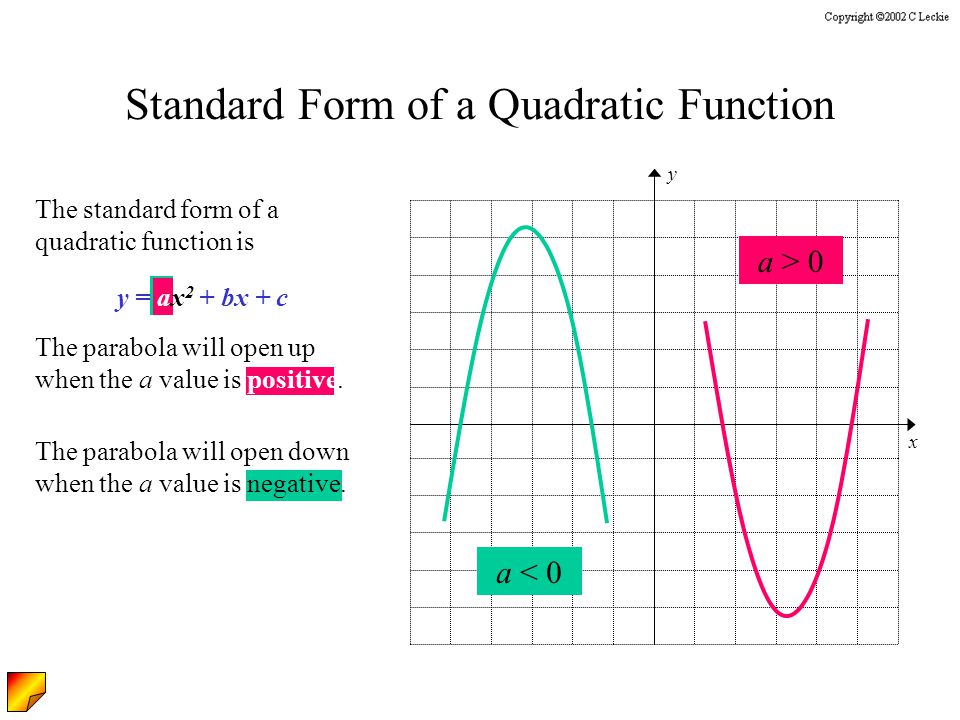
Lesson 10 2 Quadratic Functions And Their Graphs Y Ax 2 Bx C Ppt Download
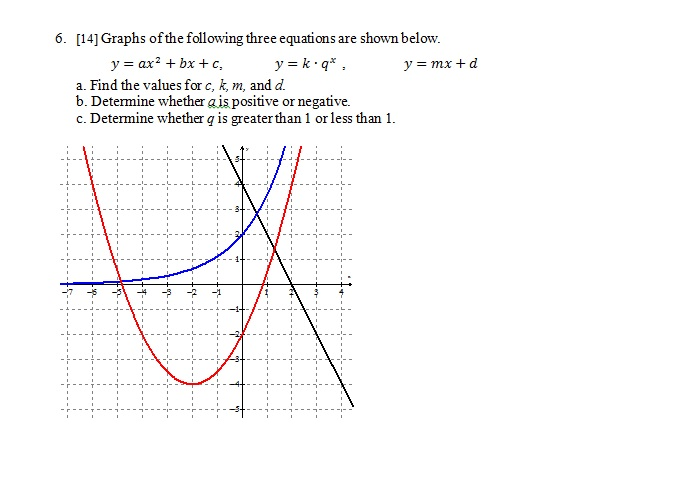
Solved Graphs Of The Following Three Equations Are Shown Chegg Com
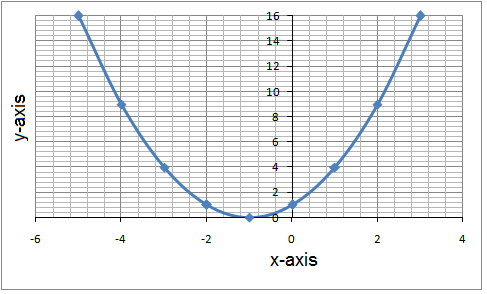
The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet
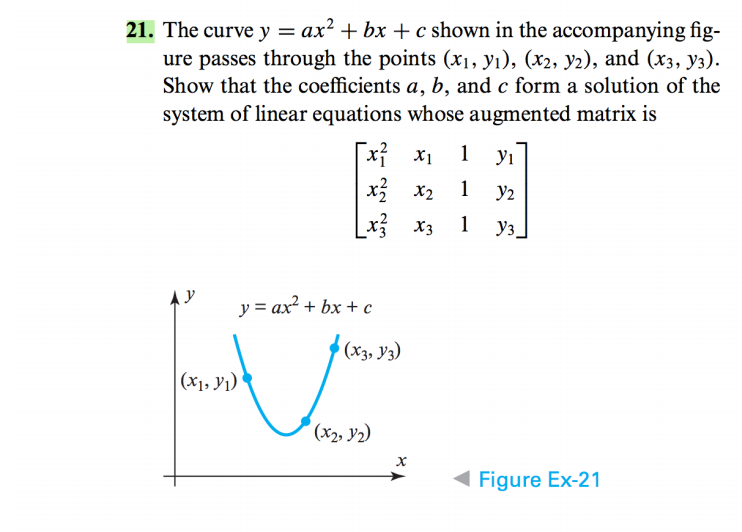
Solved The Curve Y Ax 2 Bx C Shown In The Accompany Chegg Com

Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download

Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego Pages 1 5 Text Version Anyflip

Unique Quadratic Equation In The Form Y Ax 2 Bx C

Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego Pages 1 5 Text Version Anyflip
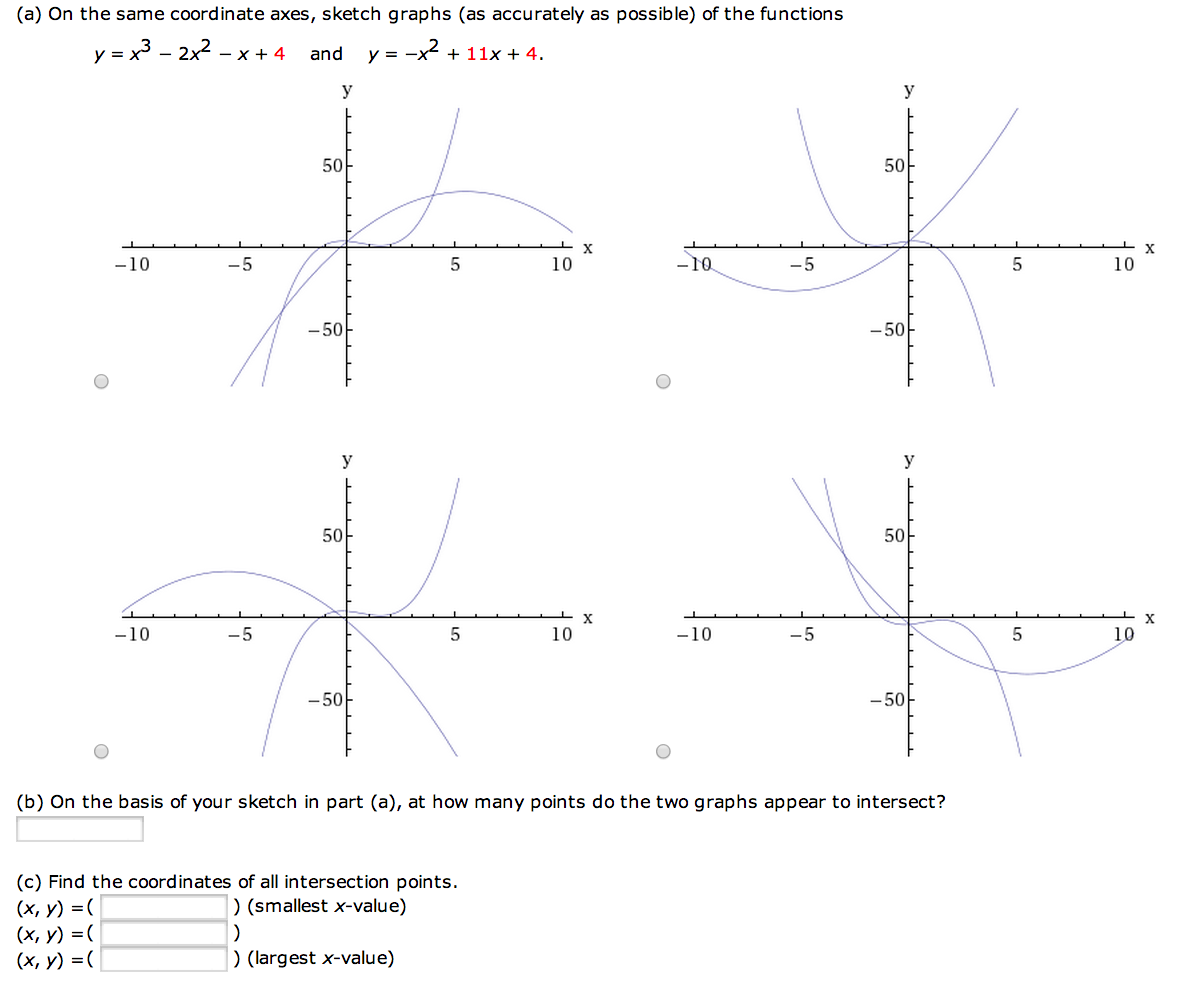
Solved Find A Parabola With Equation Y Ax2 Bx C Tha Chegg Com
Graphing Quadratic Functions
Alg 1 Graphing Y Ax2 Bx C In A Powerpoint Presentation Tpt
Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube

Prostate Gland Black And The Defined Pz Below Y Ax 2 Bx C Download Scientific Diagram

Act Math Practice Question 1184 Answer And Explanation Crackact Com
Answered Find An Equation Of The Parabola Y Bartleby

To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com

Refer The Picture Also Y Ax 2 Bx C Hd Png Download Transparent Png Image Pngitem

Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download

To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com
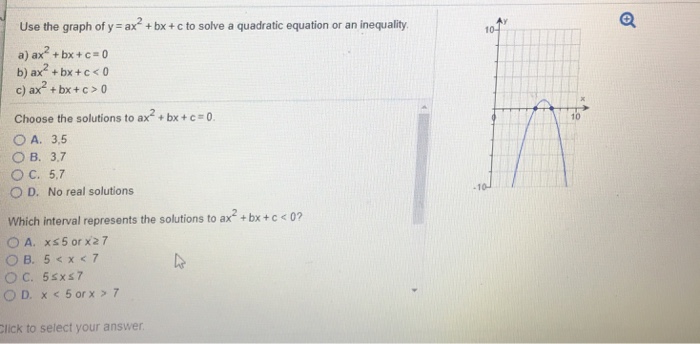
Solved Use The Graph Of Y Ax 2 Bx C To Solve A Quad Chegg Com
If The Graph Of Quadratic Polynomial Ax2 Bx C Cut Negative Direction Of Y Axis Then What Is The Sign Of C Please Answer It Fast Mathematics Topperlearning Com Psin7377
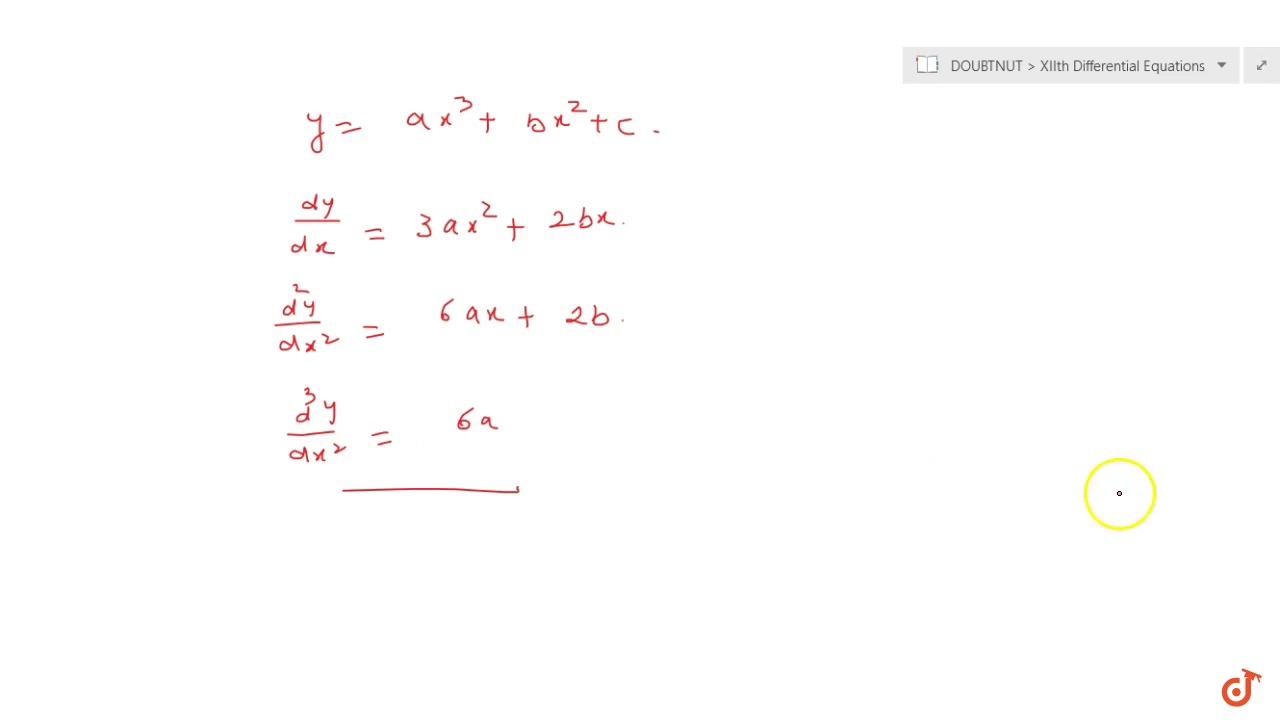
Show That Y A X 3 B X 2 C Is A Solution Of The Differential Equation D 3y Dx 3 6a Youtube
Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola

Chapter 10 Section 2 Review Quadratic Function Y Ax 2 Bx Cy 2x 2 3x 1 Symmetry Ppt Download
Quadratic Relations Y Ax 2 Bx C Between The A N B P And Download Scientific Diagram
Algebra 10 2 Graph General Quadratic Functions Y Ax 2 Bx C Math Algebra Graphing Quadratic Functions Showme

1 8 Quadratic Functions A Function F Defined By A Quadratic Equation Of The Form Y Ax 2 Bx C Or F X Ax 2 Bx C Where C 0 Is A Quadratic Ppt Download

Finding The Inverse Of Y Ax2 Bx C By Completing The Square Youtube
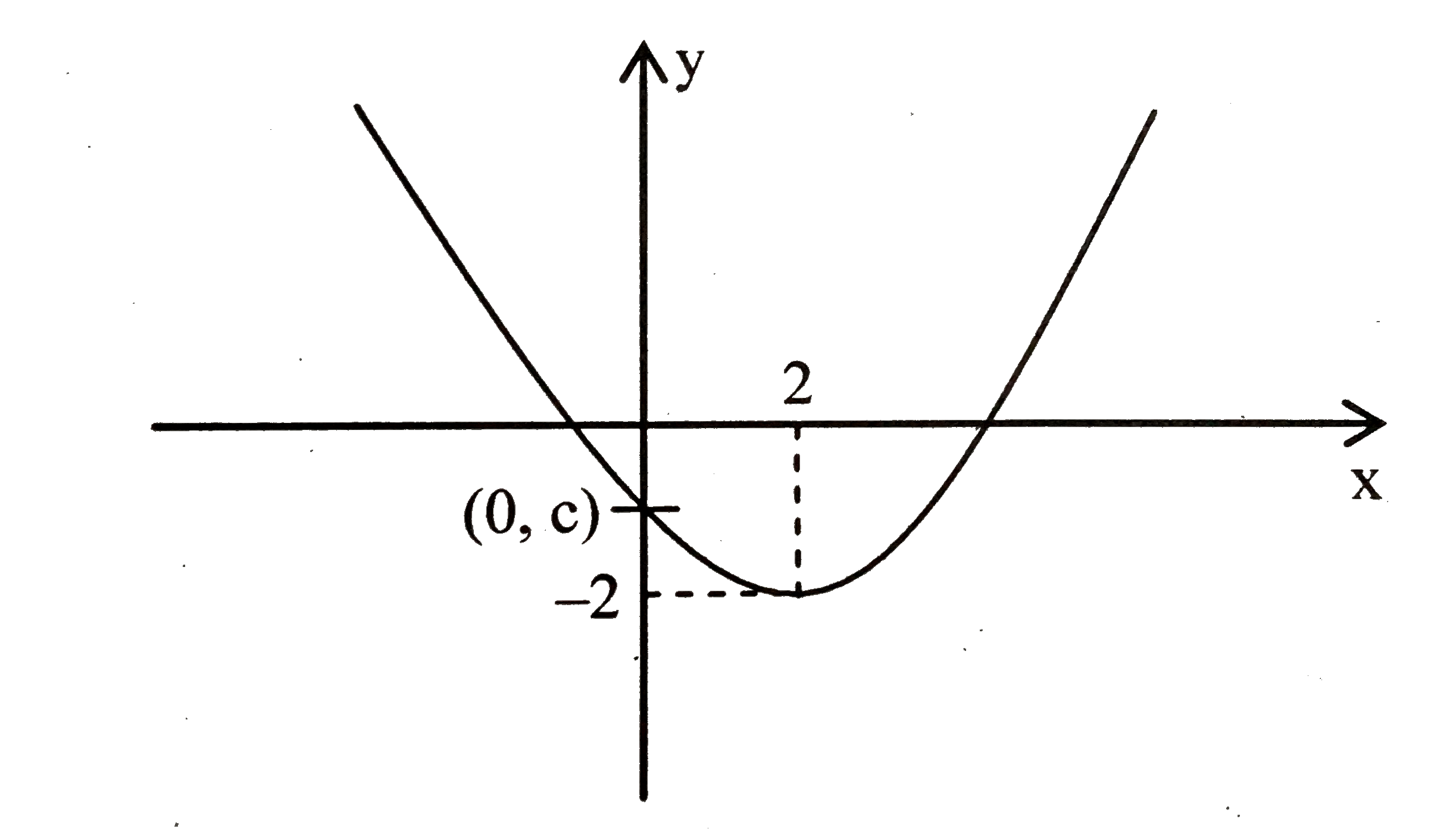
Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Pos
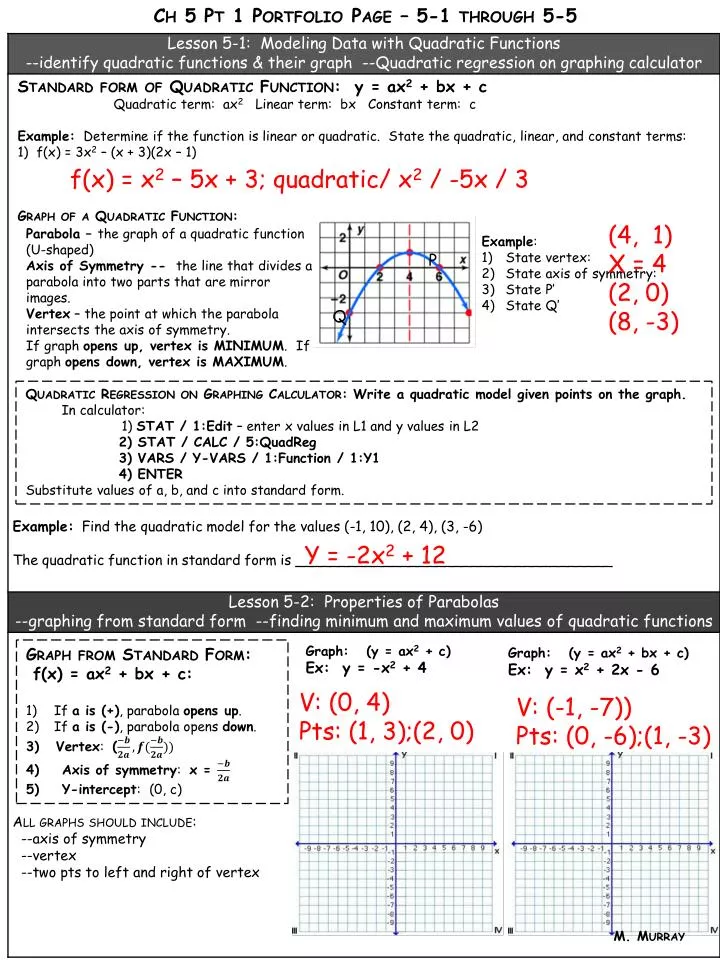
Ppt Standard Form Of Quadratic Function Y Ax 2 Bx C Powerpoint Presentation Id



